.

Il problema di Delo

…come fecero gli ateniesi a raddoppiare l’altare?

Questo problema, ossia la costruzione di un cubo avente volume doppio rispetto a quello di un cubo di spigolo dato, è uno dei tre problemi classici della matematica greca, insieme alla trisezione dell’angolo e alla quadratura del cerchio. Esistono varie leggende sulla nascita del problema della duplicazione del cubo. [Eccone una].

…

Nel racconto di Giovanni Filopono (visse nel VI d.C. ad Alessandria d’Egitto) si narra di una epidemia che imperversava ad Atene (430 a.C.) e del ricorso degli abitanti all’oracolo di Delfi per sapere fino a quando la pestilenza li avrebbe afflitti …

quando dio annunciò agli abitanti di Delfi, attraverso l’oracolo, che, al fine di sbarazzarsi della pestilenza, essi dovessero costruire un altare doppio di quello che esisteva, i loro operai specializzati caddero in una grande perplessità nei loro tentativi di scoprire come si potesse realizzare il doppio di un solido simile; essi, perciò, si recarono da Platone, per interrogarlo a proposito di ciò, ed egli rispose che l’oracolo non intendeva che il dio volesse un altare di misura doppia, ma che egli desiderava, nell’affidargli il compito, disonorare i Greci per la loro negligenza in matematica e il loro disprezzo della geometria. “Il dio ha punito il popolo per aver trascurato la scienza della geometria che è scienza per eccellenza

Esiste però un’altra versione della stessa leggenda risalente ad Eratostene (276 a.C.-194 a.C.), delle sue opere ci restano solo frammenti tramandati da altri autori, di cui riferisce Teone di Smirne (70- 135) (Expositio rerum mathematicarum ad legendum Platonem utilium, 2, 3-12 Hiller). Nel Platonico (*) Eratostene aveva raccontato di un oracolo,

…….che aveva imposto agli abitanti di Delo di raddoppiare l’altare di forma cubica, dedicato al dio. Il quesito aveva generato aporia negli “architetti”, che ne avevano cercata la soluzione, sicché i Deli avevano cercato consiglio presso Platone, che aveva interpretato l’oracolo come un rimprovero del dio agli Elleni di trascurare la geometria e un invito a occuparsene, non tanto come un’espressione del desiderio del dio di avere un altare doppio.

Un racconto analogo ricorre anche in altri testi plutarchei, precisamente De E apud Delphos (6,386 e) e De genio Socratis (7, 579 b-d), con l’aggiunta in quest’ultimo che i Deli si erano rivolti a Platone in quanto geometrikòs . Generalmente gli studiosi hanno assunto che la versione plutarchea della storia del problema di Delo sia anch’essa riconducibile al Platonico di Eratostene, ma è difficile dire se le aggiunte che essa presenta rispetto al testo di Teone risalgano anch’esse ad Eratostene o siano dovute a Plutarco stesso […]

http://crf.uniroma2.it/wp-content/uploads/2010/07/SchedaI1.pdf

.

[…]

La leggenda narra che per prima cosa gli ateniesi, di ritorno da Delfi, si recarono sull’isola di Delo e costruirono un nuovo altare, col lato doppio del precedente.

Se l era il lato dell’altare originale, il suo volume era

V=  l³

mentre il volume del nuovo altare valeva:

V′  (2l)³  8l³  8V.

.

Chiaramente la peste non cessò: gli ateniesi avevano infatti costruito un altare non due, ma otto volte più grande di quello iniziale.

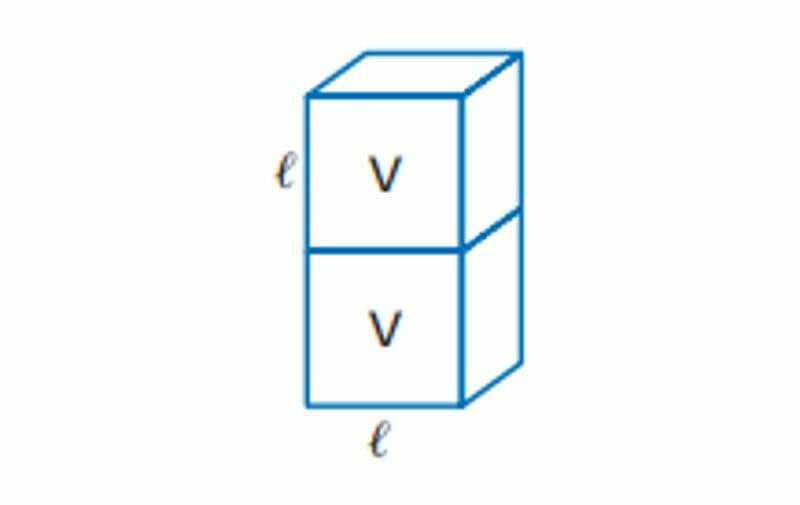
Resisi conto dell’errore, si rimisero al lavoro e costruirono un nuovo altare, mettendo sopra a quello vecchio un altro cubo delle stesse dimensioni. Anche questa volta, la peste non terminò: il volume era quello richiesto, ma l’altare non era più un cubo.

Analizziamo il problema dal punto di vista algebrico. Per costruire un altare cubico di volume doppio rispetto a quello originale deve essere

V′ = 2V →l′³=2l³

e quindi: l′ = ³√2xl

In conclusione, bisogna poter misurare un lato pari a ³√2xl

se per semplicità assumiamo l = 1, si tratta di costruire un segmento a cui corrisponda il numero ³√2.

Le regole fondamentali delle costruzioni della geometria euclidea, applicate nell’antica Grecia, permettono il solo utilizzo di riga e compasso. Tali strumenti sono ben diversi da quelli odierni: per esempio, la riga euclidea non ha unità di misura e tacche utili per misurare, ma è una semplice asta che serve solo a tracciare segmenti di retta.

Oggi sappiamo, tramite dimostrazione algebrica, che con tali mezzi è impossibile ottenere un segmento di lunghezza ³√2.

Il problema di Delo della duplicazione del cubo costituisce una delle questioni più discusse della Grecia classica. Molti matematici del tempo, come Ippocrate di Chio, Archita di Taranto e Menecmo, riuscirono a risolvere il problema attraverso metodi diversi, abbandonando comunque le regole geometriche di riga e compasso. È importante osservare che il segmento ottenuto attraverso questi procedimenti, corrispondente al numero ³√2, risulta una grandezza incommensurabile rispetto al segmento di misura 1, cioè non esiste un segmento sottomultiplo comune. Questo significa che ∛2 non è un numero razionale, ovvero non esiste alcun razionale che elevato al cubo sia uguale a 2. Si tratta quindi di un numero irrazionale.

[…]

https://online.scuola.zanichelli.it/bergamini-files/Biennio/Aperture/Ape_13_Delo.pdf

Foto: Rete

Su suggerimento del prof. Vincenzo Bloise